Warehouse Games (WHG) are inspired by a practical warehouse security scenario. The gameplay takes place on an undirected graph \( G=(V,E) \), which represents the corridors and rooms of the building.

Both the Attacker \((A)\) and the Defender \((O)\) start the game at specific vertices. In each of the \(m\) time steps, players can move to any adjacent vertex or remain in the current one. A pure strategy for player \( g \in \{O,A\} \) is thus defined as a list of vertices visited in subsequent time steps:

$$ \sigma^g = (v_1^g, v_2^g, ..., v_m^g) $$

A subset of vertices \( T \subseteq V \) is distinguished in the graph, constituting the targets. The game ends when one of the following conditions is met:

• Interception: The players are located at the same vertex at the same time. Mathematically, this condition is expressed as: $$ \exists_{i \in \{1,...,m\}} v_i^A = v_i^O $$ In this case, the Defender receives a reward \( U_{v_i}^{O+} > 0 \), and the Attacker a penalty \( U_{v_i}^{A-} < 0 \).
• Successful attack: The Attacker reaches a target \( v_i \in T \) and is not caught beforehand. This condition is written as: $$ \exists_{i \in \{1,...,m\}} v_i^A \in T \wedge \forall_{j < i} v_j^A \neq v_j^O $$ Then the Attacker receives a reward \( U_{v_i}^{A+}> 0 \), and the Defender a penalty \( U_{v_i}^{O-} < 0 \).
• Time elapsed: If neither an interception nor an attack on a target occurs within \( m \) time steps, the game ends with a payoff of 0 for both players.

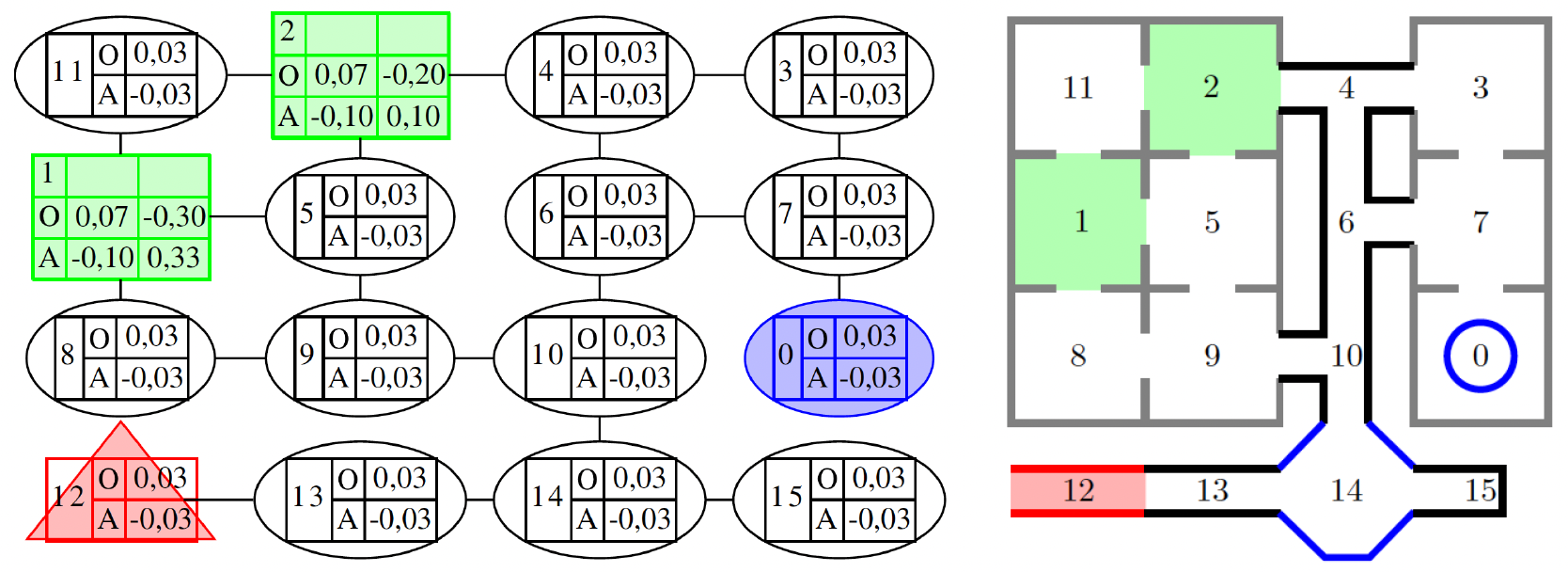
Search Games (SEG) are an extension of the concept of games on graphs. Unlike Warehouse Games, the gameplay takes place on a directed graph, and the Defender has \( k \) resource units available. A significant limitation is that these resources cannot move freely around the graph – each of them is assigned a specific subset of vertices that it can visit.

Partial Observability and Footprints

A key feature of SEG games is the partial observability of the Attacker's presence. When visiting a vertex, the Attacker leaves a "trace" (footprint) in it. This trace can be detected by the Defender in any subsequent time step if their resource visits that vertex. However, the Attacker has the ability to cover their tracks by staying in a given vertex for more than one time step.

Defender's Strategy

Due to the trace mechanism, the Defender's strategy is more complex and must define behavior both in the absence of trace detection and the reaction to finding them. Formally, a pure strategy for the Defender is defined by the formula:

$$ D = \{\mathcal{L}_{vs}^u, u \in D_u, v \in \overline{V}, s \in \{1,...,m\}\} \cup \{\mathcal{L}_{\emptyset}^u, u \in D_u\} $$

Where:

• \( \mathcal{L}_{\emptyset}^u \) – is the default list of vertices visited by resource \( u \) in the absence of trace detection.
• \( \mathcal{L}_{vs}^u \) – is the list of vertices visited by resource \( u \) from the moment a trace is detected at vertex \( v \) in time step \( s \).

The Defender executes the default strategy until the first trace is detected, after which they switch to the appropriate reaction strategy.

Game Termination Conditions

The rules for assigning payoffs and ending the game are analogous to Warehouse Games:

• Capture: Defender and Attacker are in the same vertex at the same time.
• Attack success: Attacker reaches a target (unnoticed by the Defender in the same step).
• Time up: None of the above events occur within the limit of \( m \) steps.

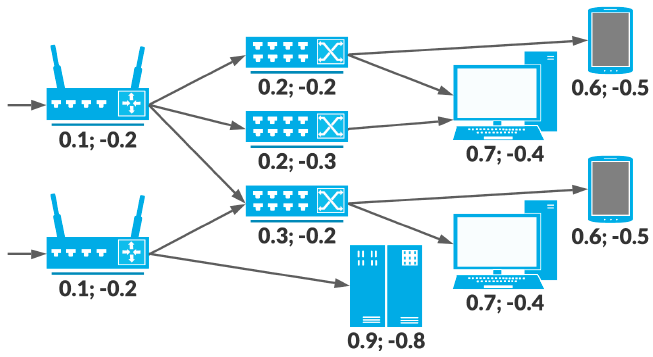
FlipIt Games (FIG) were inspired by cybersecurity scenarios. They model a situation in which the Attacker tries to take control of network infrastructure elements (e.g., routers, servers), and the Defender takes actions aimed at regaining control over them.

Gameplay Overview

The game takes place on a directed graph for a specified number of time steps \( m \). In each step, players perform an action consisting of choosing one vertex over which they attempt to take control (a so-called flip). At the beginning of the game, all vertices are controlled by the Defender, and the Attacker has access only to selected "entry vertices".

Control Takeover Rules

The mechanics of resource takeover are crucial for this type of game:

• The takeover operation is successful only if the player already controls at least one preceding vertex (from which an edge leads to the target) or if an entry vertex is being attacked.
• If both players try to take over the same vertex at the same time, its state does not change (it remains under the control of the current owner).

Payoff Model

Unlike other games, here the payoff is calculated cumulatively. Each vertex \( v \) is assigned a reward for possessing control \( U_{v}^{+} > 0 \) and a cost for performing a takeover action \( U_{v}^{-} < 0 \). The total payoff for player \( g \) is expressed by the formula:

$$ U_{g} = \sum_{s \in \{1,...,m\}} \sum_{v \in R_{s}(g)} U_{v}^{+} + \sum_{s \in \{1,...,m\}} U_{v_{s}^{g}}^{-} $$

Where:

• \( R_{s}(g) \) – the set of vertices controlled by player \( g \) after step \( s \).
• \( v_{s}^{g} \) – the vertex on which player \( g \) performs an action in step \( s \).

No Information (No-Info)

A significant aspect of the game is the lack of full knowledge about the state of the game. Players do not know during the game which vertices they actually control. They must plan their strategy (the sequence of moves for the entire game) at the very beginning and cannot change it during the gameplay.

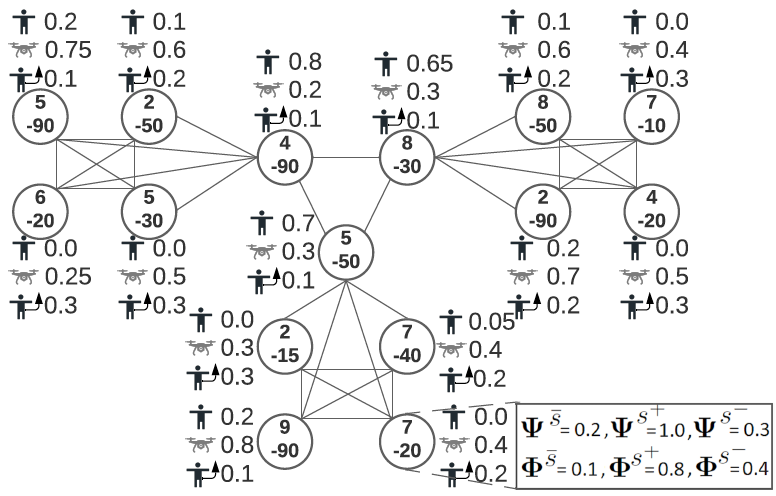
Signaling Games (or Security Games with Signaling) belong to the family of Green Security Games and are inspired by environmental protection problems, such as combating poaching in national parks.

Diverse Resources

A distinguishing feature of SGS is the division of Defender resources into two categories with different functions:

• Drones (\( k_d \)): Used for monitoring and detecting threats. They can send signals but cannot independently capture the Attacker.
• Rangers (\( k_s \)): Can move and intervene (capture the Attacker).

Gameplay Flow and Signaling

The game consists of several stages. After both players choose their strategies and an attack on a chosen target occurs, if a drone is present at the vertex, it can send one of two signals:

• Weak signal (\( s_0 \)): A silent piece of information sent to rangers about a detected threat (without alerting the Attacker).
• Strong signal (\( s_1 \)): Triggering light and sound signals to deter the Attacker (in addition to notifying rangers).

Upon receiving a signal, a reallocation phase follows, in which rangers from neighboring vertices can move to the attacked target to thwart the attack.

Uncertainty

The SGS model introduces two key types of uncertainty that complicate the decision-making process:

1. Detection uncertainty (\( \gamma \)): Automated detection systems in drones are unreliable. There is a probability \( \gamma \) that a drone present at the attacked vertex will not detect the threat.
2. Observation uncertainty (\( \Omega \)): The Attacker may misinterpret the situation. The matrix \( \Omega \) defines the conditional probabilities with which the Attacker will observe a given signal (or lack thereof), depending on what the drone actually sent.

Strategies

The Defender's strategy is complex in this model. It includes not only the allocation of drones and rangers but also a reallocation plan (reaction to reports) and a signaling plan – i.e., the probabilities of sending signals \( s_0 \) or \( s_1 \) depending on whether the drone detected an attack or not.